Article by Khayla Black
Answer: The membrane potential is voltage difference across the neuronal membrane which is established as a result of chemical and electrical forces acting on the membrane.
Voltage must be carefully regulated across the membrane in order to prevent drastic cellular malfunctions within neurons. This regulation is ensured by maintaining a specific distribution of charge across the cell.
The neuronal membrane contains many proteins; an important class of these proteins are ion channels. Ion channels spanning the membrane consist of various subunits which exhibit remarkable specificity. Each channel has a specific diameter and set of R groups lining the inside, allowing very specific ions to enter and pass through the channel.
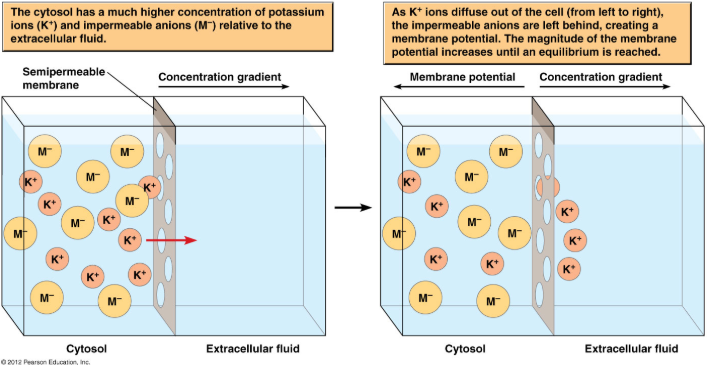
Once the ion channels open, movement is regulated by chemical and electrical forces. Varying concentrations of an ion on both the outside and inside of the cell establish a concentration gradient across the membrane. Ions tend to diffuse down their concentration gradients via ion channels; however, once ions begins to build up on one side of the cell, charge begins to accumulate. For example, potassium is highly concentrated inside the cell, so it will travel down its concentration gradient to the outside of the cell. Once this happens, positive charge begins to build up, and ions experience an electrostatic force, pulling them back into the cell. Thus, chemical gradients and electrostatic forces will work simultaneously to make what is commonly referred to as an electrochemical gradient.
Diffusion, attraction, and repulsion, will all continue to drive ions across the membrane, and eventually, the cell will come to a point where the electrical force is equal to the chemical force on the ion. The potential at which this occurs is known as the equilibrium potential.
The membrane potential in neurons is mainly governed by four ions: Na+, K+, Ca2+, and Cl-. Each individual ion has its own equilibrium potential that contributes to that of the entire membrane. If the concentration on the ion is known for both the inside and outside of the cell, the equilibrium potential can be calculated using an equation known as the Nernst Equation (shown below). This equation (derived from Gibbs free energy under standard conditions) provides the equilibrium potential of a single ion given the concentration of the ion inside and outside of the cell along with the charge on that ion.
Nernst equation
Individual equilibrium concentrations are essential to understanding how the influx/efflux of ions will influence the neuron. The equilibrium potentials for the most common ions are as follows:
Sodium (Na+): 62 mV
Calcium (Ca2+): 123 mV
Chloride (Cl-): -65 mV
Potassium (K+): -60 mV
Despite the usefulness of the Nernst equation, it does have it’s limitations. Since the membrane is permeable to a variety of ions, it is occasionally useful to take this into consideration when performing calculations. The Goldman equation does exactly this by utilizing the relative membrane permeability of multiple ions (PK and PNa).
Goldman equation
Using the Goldman equation, a sample calculation can be done to estimate the equilibrium potential of the neuronal membrane.
Thus, when the electrical and chemical forces are balanced, the membrane potential is approximately -65 mV. The threshold potential for generation of an action potential is -55mV, so we can imagine why the influx of ions is so essential to neuronal function and communication. When ions enter the cell, they will try to bring the membrane potential towards their equilibrium potential. Thus, the entrance of sodium into the cell drives the potential towards its equilibrium potential (62mV). With a great enough influx of sodium, the membrane potential will be driven towards the threshold value. This explains the depolarizing effect that sodium has on the membrane. A similar situation occurs for potassium. The equilibrium potential for potassium is approximately -80, so the entrance of potassium into the cell will drive the neuron further away from threshold and is said to hyperpolarize the cell.
Regulation of ions is key to ensuring proper neuronal function, as dysregulation can result in detrimental effects such as excitotoxicity. Understanding the neuronal membrane allows scientists to gain insight into numerous diseases, and is also key to understanding chemical transmission between neurons.